Laboratory of Solid State Theory
The main investigation area of the laboratory is condensed matter theory. New methods for numeric modeling of solids are developed with the aim of investigating and predicting properties of crystals, glasses, hetero- and nanostructures. In particular, we consider
- magnetic phenomena and quantum oscillations of high temperature superconductors,
- nonlinear dynamics of crystal lattice,
- vibration solitons and crystal defect formation in application to material radiation resistance,
- graphene and carbon nanotube complex structures,
- singular and nonlinear quantum optics.
People
| Artjom Vargunin Head of Laboratory, Associate Professor in Solid State Theory E-mail: artjom.vargunin@ut.ee Kabinet: B306 CV, projects: ETIS Publications: Scopus |
|
| Vladimir Hizhnyakov Academician, Associate Professor in Solid State Theory E-mail: vladimir.hiznjakov@ut.ee Office: B305 CV, projects: ETIS Publications: Scopus |
|
| Pavel Rubin Associate Professor in Solid State Theory E-mail: pavel.rubin@ut.ee Office: B309 CV, projects: ETIS Publications: Scopus |
|
| Alexei Sherman Associate Professor E-mail: aleksei.serman@ut.ee Office: B317 CV, projects: ETIS Publications: Scopus |
|
| Teet Örd Professor emeritus E-mail: teet.ord@ut.ee Office: B316 CV, projects: ETIS Publications: Scopus |
|
| Küllike Rägo Research Fellow in Field Theory E-mail: kullike.rago@ut.ee Office: B313 CV, projects: ETIS Publications: Scopus |
|
| Alexander Shelkan Research Fellow in Solid State Theory E-mail: aleksander.shelkan@ut.ee Office: B310 CV, projects: ETIS Publications: Scopus |
|
| Vadim Boltrushko Research Fellow in Solid State Theory E-mail: vadim.boltrushko@ut.ee Office: B310 CV, projects: ETIS Publications: Scopus |
|
| Aleksandr Pishtshev Research Fellow in Solid State Theory E-mail: aleksandr.pishtshev@ut.ee Office: B306 CV, projects: ETIS Publications: Scopus |
Current research projects and networks
- Personal research funding "Spectroscopy of entangled states of clusters of rare-earth impurity ions for quantum computing" (2019-2023) PRG347, Yury Orlovskiy.
- Returning researcher grant "Flux-flow based spintronics in superconducting heterostructures" (2019−2021) MOBTP152, Artjom Vargunin.
- Institutional Research Funding "Nonlinear theory of solids and fundamental fields" (2013-2018) IUT2-27, Vladimir Hižnjakov.
Selected publications
- V. Hizhnyakov, V. Boltrushko, H. Kaasik, Yu. Orlovskii, Rare Earth Ions Doped Mixed Crystals for Fast Quantum Computers with Optical Frequency Qubits, Optics Communications 485, 126693 (2021)
- Y. Orlovskii, H. Gross, E. Vinogradova, V. Boltrushko, V. Hizhnyakov, Spectroscopic evidence of cooperative (entangled) quantum states of Nd3+ ion pairs in Nd3+:LaF3 crystal, Journal of Luminescence 219, 116920 (2020)
- A. Vargunin, M. Silaev, Magnetic field-controlled 0−pi transitions and their experimental signatures in superconductor-ferromagnet-superconductor junctions Appl. Phys. Lett. 116, 092601 (2020)
- A. Vargunin, M. Silaev, E. Babaev, Unusual resistive states of multiband superconductors in the effective field theory approach, EPL 130, 17001 (2020)
- A. Vargunin, M. Silaev, Flux flow spin Hall effect in type-II superconductors with spin-splitting field, Sci Rep 9, 5914 (2019)
Theoretical materials physics
Using specialized modern computer hardware and software, we apply powerful ab initio computational methods in order to simulate the electronic and vibrational structure of solids, lattice dynamics, and to study chemical bonding. This approach provides comprehensive information about physical processes of interest and allows us to perform theoretical investigations for prediction of material properties.

Figure 1. Features of chemical design in ABO2 delafossite-type crystals.
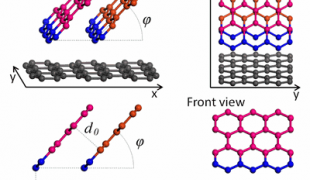
Various carbon-based structures have been studied in recent years. The numerical modelling of graphene strips and structures of carbon nanorods showed that the correct choice of strips and rods allows one to create structures with different properties. For instance, the right choice of sizes makes it possible to obtain ultralight materials. In particular, these structures can be used as electron memory elements.
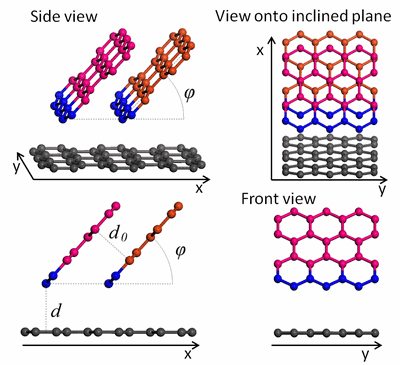
Figure 2. Zigzag-type carbon nanocrystals and graphene nanorods.
High-temperature superconductivity
The most interesting category of crystals with strong correlations is high-temperature superconductors - compounds that have near zero electrical resistance at high temperatures - up to -135 C in some crystals. The properties of such crystals are unusual, including magnetic properties, where they demonstrate unusual structures in the magnetic moments of atoms. The reason for these unusual properties are strong electron correlations - unlike other crystals, the highest energy is not the energy of electron movement but rather on-site Coulomb repulsion between electrons. In cooperation with the University of Stuttgart, we succeeded to establish theoretically that a special property of high-temperature superconductors caused by strong electron correlations is the nanoscale phase separation. This property was confirmed experimentally in cooperation with the Nobel prize winner, discoverer of high-temperature superconductivity A. Müller and R. Kremer from the Max Planck Institute in Stuttgart.
We have long lasting experience in the theory of multi-component (in many cases high-temperature) superconductors where the account of interactions between different electron subsystems is of decisive importance. The varied physics reflected by the properties of these compounds with complex structure has been an object of growing interest in the world. By now the multi-gap superconductivity has been established in a number of compounds such as NbSe2, V3Si, Nb-doped SrTiO3, ruthanates, heavy fermion systems, MgB2, copper oxides, iron-pnictides, iron-chalcogenides etc. We have developed the multi-band scenario for cuprate superconductors and magnesium diboride. In the multi-component superconductivity, the following problems are continuously actual for us:
- The peculiarities of the spatial behavior in mesoscopic scale which are substantially different from the observations in one-component superconductors
- Thermodynamic properties and fluctuation effects
- Mutual influence with other electromagnetic orderings
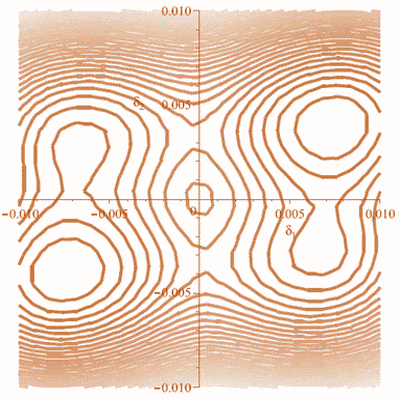
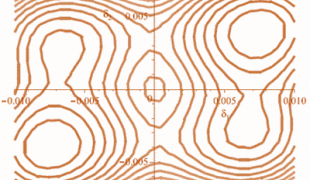
Figure 3. The contour plot of the free energy of a two-band superconductor as a function of non-equilibrium order parameters. One can observe the presence of characteristic stable and metastable minima.
Random processes
- The stochastic effects in phase transitions (e.g. ferroelectric and ferromagnetic materials) are of interest. We have demonstrated the complementarity of phase transition and stochastic resonance in spatially restricted systems. The crossover from stochastic resonance to phase transition and vice versa controlled by the dimensions of the sample has been established.
- The modelling of the transport of vortices in superconducting systems (including type-1.5 superconductors) taking into account the factors of noise.
- The modelling of the stochastic properties of Josephson contacts in the case of one-band and two-band superconductors.
Investigations of strongly correlated electron systems
Crystals characterized by strong electron correlations are high temperature superconductors - cuprate perovskites and ferro-pnictides, heavy fermion and low dimensional organic compounds. Due to unusual properties and in view of their technological applications these crystals are one of the central topics of the contemporary theory of solids. In our laboratory new theoretical methods were developed for investigating these crystals, including the theory of magnetic properties of p- and n-type cuprate perovskites and the strong coupling diagram technique, which allowed us to suggest an explanation for low-frequency quantum oscillations observed in lightly doped cuprates.
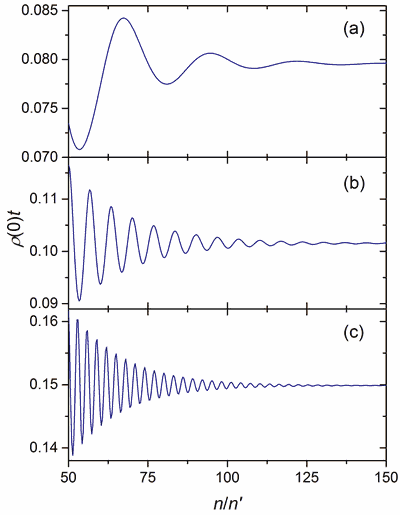
Figure 4. The change of the quantum oscillation frequency with doping of a crystal with strong electron correlations. The parameter n/n’ is inversely proportional to magnetic induction.
Two-dimensional frustrated magnets
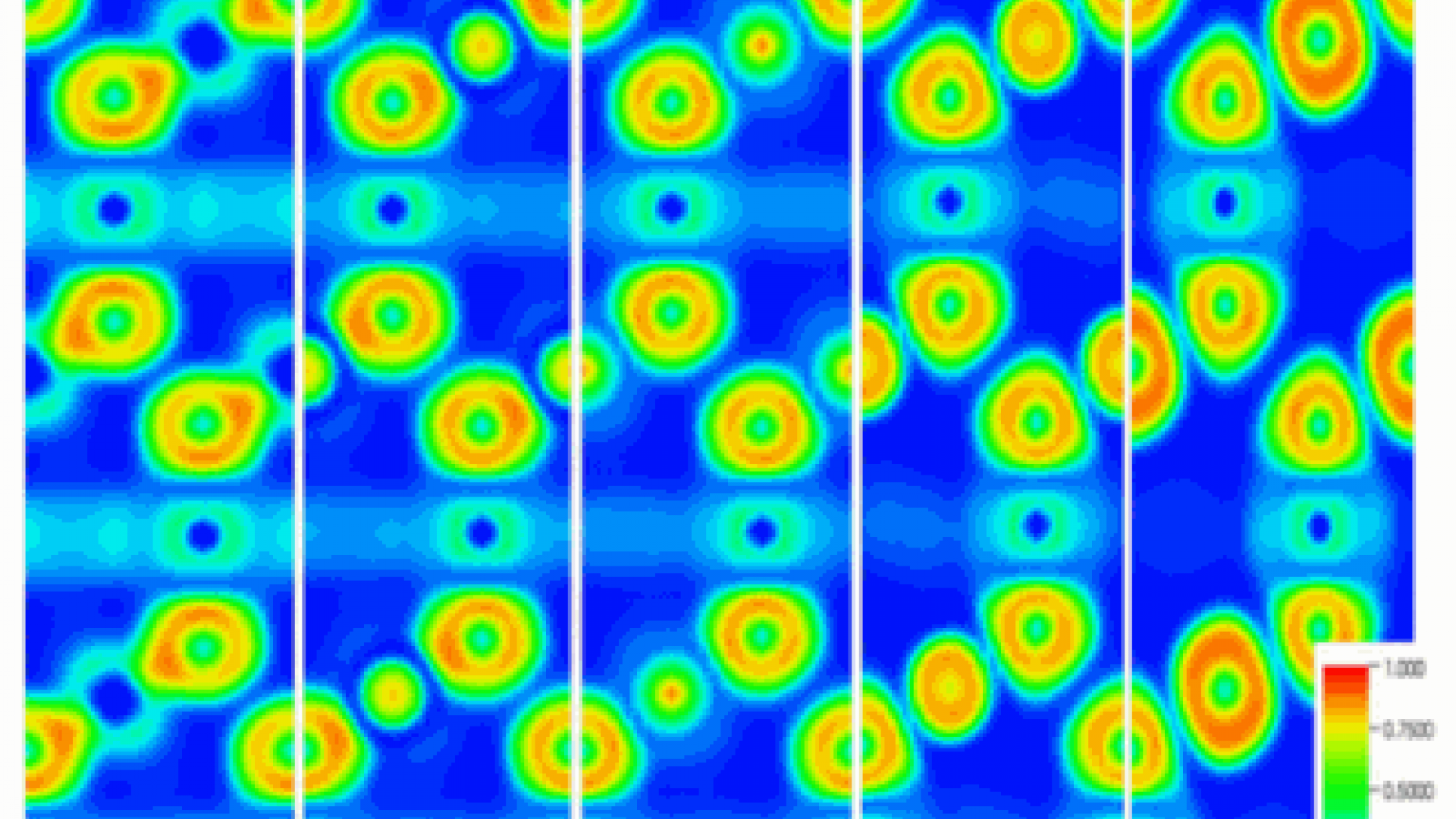
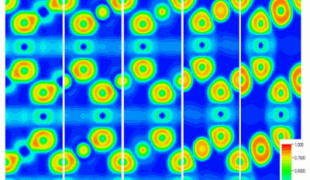
The interest to frustrated magnet compounds is connected with their rich phase diagram. Recently synthesized crystals of this class demonstrate interesting properties. Among them the crystal NiGa2S4 can be mentioned. In this compound, Ni ions with the spin S=1 form quasi-two-dimensional triangular lattice. With the use of Mori’s projection operator technique we have investigated the phase diagram and magnetic excitations of this crystal in the framework of the J1-J3 model. Dispersions of magnetic excitations for different values of the frustration parameter p are shown in the figure. It was found that the phase diagram contains regions without magnetic ordering as well as with long-range ferromagnetic and antiferromagnetic orderings. Depending on the frustration parameter the antiferromagnetic ordering is commensurate or incommensurate. Obtained results allow us to explain a number of experimental observations in NiGa2S4.

Figure 5. Dispersions of magnetic excitations for different values of the frustration parameter p.
Vibrational solitons in crystals
Spatially localized vibrational modes may exist not only in lattices with point defects but also in perfect nonlinear lattices. Frequency of such modes lies outside the phonon spectrum, which prevents the spreading of the vibrations to the bulk. We have numerically studied such vibrational solitons - breathers, their existence conditions and properties for different types of lattices. It was found that these excitations may exist in simple monoatomic crystal lattices, having frequency above the phonon spectrum. Examples are given by simple metals Fe, Cu, Ni, Nd and dielectrics, e.g., diamond.
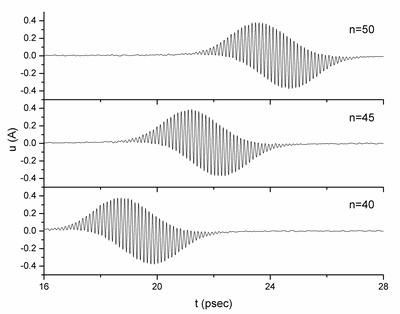
Figure 6. Breather in Cu lattice - displacements of n-th atom (in Angstroms) vs time (in picoseconds).
Efficient energy transmission in metals
The practical use of solid-state materials is largely determined by the energy transfer taking place within them. Molecular dynamics methods have been used to study vibrational excitations in metals. It has been found that vibrational solitons in metals, discovered by us, are highly mobile and may transfer energy, which is hundreds times larger than the oscillating quantum of thermal energy at room temperature, at distances of thousands lattice spacings. To this point a comparable efficiency of energy transfer was only known in dielectrics, where it originates from the spread of electron excitations.
Formation of defects in crystals
A method was developed to model the formation of defects in crystal lattice structures, which allowed us to consider the dynamics of macroscopic crystals taking into account long-range interactions. It turned out that the latter interactions stimulate defect formation in crystals. It means that if these interactions are switched off, which is possible using dispersed enough matter, we can significantly increase the radiation stability of materials. If this conclusion is confirmed in experiments, we will be able to take another step toward resolving this very significant problem in nuclear energetics.
Multifunctional materials
In multifunctional systems ferroelectricity, (anti)-ferromagnetism, ferroelasticity and elasticity coexist in a single compound. In these substances the strong vibronic interaction is a leading coupling, being the stabilizing force in phase transitions. We have developed a semi-microscopic theory for quantum paraelectrics and quantum ferroelectrics (SrTiO3, KTaO3, etc.). Photo-induced phase transitions have been studied, including ferroelectrics and, in particular, perovskites.
The Jahn-Teller effect and conical intersection of potential surfaces
In molecular systems, there often arise situations where two potential surfaces intersect and form conical-shaped potential cross-section. The vicinity of these sections ("funnels") displays strong mixing of electronic and vibrational states. As a consequence the states cannot be considered as independent, which poses a complicated physical problem.
The above-mentioned mixing significantly increases the speed of chemical and photochemical reactions as well as the rate of the nonradiative transition from excited to ground state. Conical intersections are present in many biomolecules, for example, in DNA, where they play an important role in determining biochemical properties of those molecules.
Due to the importance for applications, this molecular dynamics problem has been the object of intensive research. However, thus far there has been no precise physical description for this process. Recently we have developed its rigorous quantum mechanical description, which allowed us to visualize in details the molecular system evolution through the conical potential intersection.
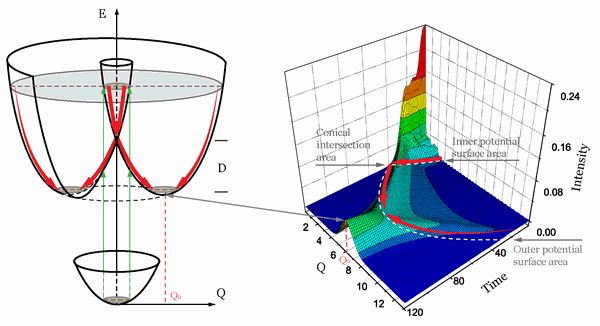
Figure 7. Left: conical intersection in the Jahn-Teller effect. Right: relaxation of the wave packet of a Jahn-Teller active vibration.
Optical properties of quantum liquids helium-3 and helium-4
In modern physics, the Fermi and Bose type quantum liquids helium-3 and helium-4 at extra low temperatures and pressure are an object of interest due to their unique properties. The droplets of helium liquids are usually studied by spectroscopic methods with doping the droplets by small molecules. In collaboration with G. Benedek from the Milano-Bicocca University it was shown that in the spectrum of sodium molecule trapped at the surface of helium-4 droplets the surface vibrations of the quantum liquid and the kinetic zero-point energy of the neighbor helium-4 atoms reveal themselves.
In the Fermi liquid of helium-3 a unique mechanism of interaction of electronic excitations with nuclear motion was discovered: in optical spectra of glyoxal molecule inside helium-3 droplet the surface excitations of the Fermi sea are directly observable. The corresponding spectra were calculated.
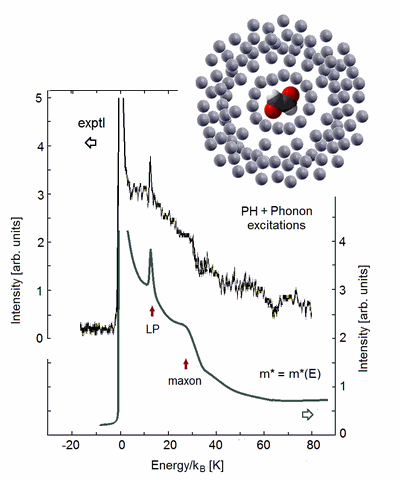
Figure 8. Optical spectrum of glyoxal molecule in helium-3 droplet. Besides the phonon excitations the surface excitations of the Fermi sea are shown.
Multi-stage absorption of short coherent light pulses
Due to improvements in experimental possibilities the accuracy in studying the interaction between matter and light pulses increased significantly. The absorption of several light pulses and the persistent spectral hole burning with these pulses are of interest. We are developing the time dependent theory of multi-stage absorption, which is applicable for pulses of arbitrary length, starting from femtosecond to practically stationary ones. The time delay between these pulses can be also arbitrary - from their full coincidence to full separation. We have already applied this theory to the persistent spectral hole burning.
Spectroscopy of single molecule
In experiment, different widths of a purely electronic zero-photon line are observed for identical single molecules embedded in the same host crystal. Anisotropy of a birefringent host crystal is one of the reasons for this phenomenon. We have developed a theory, which takes into account the dependence of the spontaneous emission rate and, consequently, the dependence of the radiative linewidth of a single-impurity molecule on the orientation of the electronic position vector (or the transition dipole moment vector in the dipole transition) in the crystal.
Quantum optics: a new source of entangled photons
A source of a new type of entangled photons has been proposed. It relies on the strengthening of interaction between light and matter due to plasmonics. The source is based on two effects: 1) resonant amplification of bi-photonic radiation in a situation where the amplitude of the oscillation of optic length equals the wavelength of generating photons; 2) strengthening of interaction between light and matter due to plasmons on the metal-insulator interface. The evaluations of the effectiveness of the new source of photons exceed the efficiency of standard sources by several orders of magnitude.
It was shown that plasmonics allows one to enhance strongly (by many orders of magnitude) the dynamical Casimir effect, which until now was not observed in optics but is very important phenomenon for fundamental background of modern physics.
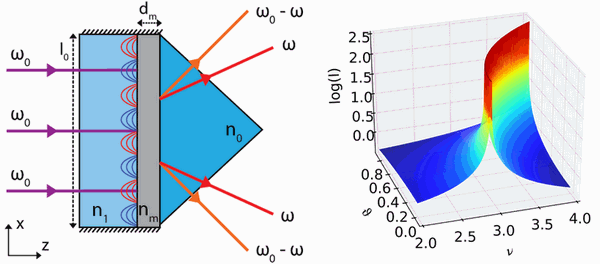
Figure 9. The experimental set-up for observation of the dynamical Casimir effect in a metal-dielectric interface placed to the resonator (left). The Kretschmann prism is used to transform generated surface plasmon polaritons to photons. Here ω0 is the frequency of laser excitation, ω and ω0-ω are frequencies of generated photons. In the right figure the intensity of generated photons as a function of laser field E0 ∝ ν and emission angle ϑ is given.
Energy of vacuum
According to quantum mechanics, the foundation of modern physics, there is a number of various contributions into the energy density of a vacuum. The largest contribution is provided by quantum fluctuations of the zero state of fundamental bosons. The energy density is huge, of the order of the Planck energy density of 4.63x10113 J/m3, which exceeds the observable energy density of a vacuum by about 10120 times. V. Hizhnyakov studied the possibility of compensating the huge zero energy of bosons in a vacuum and demonstrated that the needed compensation comes from quantum particle gravitational energy. Namely, quantum particles cause fluctuations with negative energy on the Planck scale, while on fluctuations smaller than the Planck length, an internal repulsive interaction is predominant in particles. The repulsion interaction parameter yields a Higgs boson mass value of 123 GeV, which agrees with the latest measurements.
International collaboration: Max Planck Institute for Solid State Research, Stuttgart; Chemnitz University of Technology, Brandenburg University of Technology, Milano Bicocca University, University of Seville, Kharkov Institute of Physics and Technology, Kirensky Institute of Physics (Russian Academy of Sciences, Krasnoyarsk).
Collaboration in Estonia: Center of excellence "Mesosystems - theory and applications", Tallinn University of Technology.
- Scientists' discovery is paving the way for novel ultrafast quantum computers - Phys.org, Jan. 2021